Problema del Viajante de Comercio

Vamos a explicar brevemente el modelo del TSP cómo un problema de programación lineal entera. Para ello recordamos que el planteamiento inicial y puramente intuitivo: 

"Un viajante debe recorrer \(n\) ciudades, pasando solo una vez por cada una de ellas ¿Cómo debe ser el recorrido, para que la distancia sea mínima ?"

Sea \(n\in\mathbb{N}\) el número de ciudades a recorre y sea  \((V,E)\) un grafo, en el que \(V\) es el conjunto de las \(n\) ciudades y \(E\) las aristas o caminos entre estas. Nuestras variables de decisión serán:

\( x_{i,j} = \left\{ \begin{matrix} 1 & \text{si se toma el arco } (i,j) \\ 0 &\text{en caso contrario} \end{matrix} \right. \) 

Además cada arista \((i,j)\in E\) del grafo tendrá asociada la distancia \(d_{i,j}\) entre las ciudades \(i\) y \(j\). Cómo nuestra intención es minimizar la distancia nuestra función objetivo será:

\(\sum\limits_{i,j=1}^n d_{i,j}x_{i,j}\)

Donde si \(i=j\) o si \((i,j)\notin E\) se pondrá \(M\) .

Además se requiere que se pase por todas las ciudades, solamente una vez. Esto puede interpretarse como que el número de aristas, en el camino solución, que llegan a y salen de cada vértice solo ha de ser 1. Esto se traduce en:

\( \left. \begin{matrix} \sum\limits_{j=1}^{n} x_{i,j} = 1 &, i = 1,...,n\text{ (Aristas que llegan)}\\ \sum\limits_{i=1}^{n} x_{i,j} = 1 &, j = 1,...,n \text{ (Aristas que salen)}  \end{matrix} \right. \)

Sin embargo, aún falta algo más para que esté bien modelado ¿Sabes qué falta?. Observa que si solamente dejásemos las dos restricciones anteriores cabe la posibilidad de aparezcan soluciones con subrutas, es decir algo como lo que ocurre en la siguiente imagen (creada con graphdrawer): 

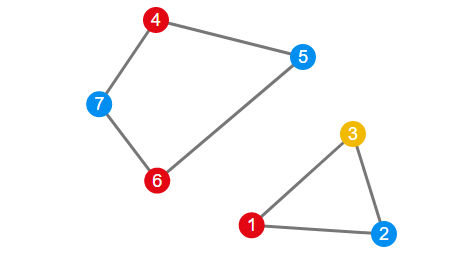
Por lo que necesitaremos una restricción que impida que este tipo de soluciones sean factibles

\( u_i - u_j + nx_{i,j}\leq (n-1) , 1< i \neq j\leq n \)

Y así queda nuestro modelo final del TSP:

\( \left. \begin{matrix}\text{min} & \sum\limits_{i,j=1}^n d_{i,j}x_{i,j}&\\  \text{s. a} & \sum\limits_{j=1}^{n} x_{i,j} = 1 &, i = 1,...,n\\ &\sum\limits_{i=1}^{n} x_{i,j} = 1 &, j = 1,...,n \\ & u_i - u_j + nx_{i,j}\leq (n-1) &, 1< i \neq j\leq n\\ & x_{i,j}\in\{0,1\},u_i,u_j\in\{1,...,n\} \end{matrix} \right. \)

¡ QUÉ BONITO !