El viajante de comercio

Éste es uno de los problemas de optimización más estudiados hasta el momento.

Una solución directa, óptima, puede ser intentar todas las permutaciones posibles y ver cuál es la mejor, pero no es operativo, ya que conduce a problemas muy grandes e ineficientes desde el punto de vista del tiempo de ejecución del problema. Es impracticable para más de 20 ciudades.

Es por eso que intentaremos el uso de métodos que dan solución aproximadas. Normalmente se utilizan métodos heurísticos para resolverlos; algoritmos que no garantizan una solución óptima, pero suelen encontrar soluciones aproximadas al óptimo. Nos centraremos en éstos.

Nuestro problema puede enunciarse del siguiente modo: Un viajante de comercio ha de visitar \( n \) ciudades, comenzando y finalizando en su propia ciudad; conociendo el coste de ir de cada ciudad a otra, determinar el recorrido de coste mínimo.

Propiedades de los algoritmos heurísticos

Un buen algoritmo heurístico debe tener las siguientes propiedades:

1. Eficiente. Debe tener un esfuerzo computacional realista para obtener la solución.

2. Bueno. La solución debe estar, cerca del óptimo.

3. Robusto. La probabilidad de obtener una mala solución; es decir, que se encuentre lejos de la óptima; debe ser baja.

Para medir la calidad de un heurístico existen diversos procedimientos:

• Comparación con la solución óptima: Aunque normalmente se recurre al algoritmo aproximado por no existir un método exacto para obtener el óptimo, en ocasiones podemos usarlo para un conjunto limitado.

• Se mide para cada uno de los ejemplos la desviación porcentual de la solución heurística frente a la óptima. Si llamamos \( c_{sh} \) al coste de la solución del algoritmo heurístico y \( c_o \) al coste de la solución óptima, en un problema de minimización la desviación porcentual viene dada por: \( \frac{c_{sh}-c_o}{c_o}100 \)

• Comparación con una cota: En ocasiones la solución óptima no es posible ni siquiera para un conjunto limitado. Un método alternativo de evaluación consiste en comparar el valor de la solución del heurístico con una cota del problema (inferior si es un problema de minimización y superior si es de maximización).

• Comparación con otros heurísticos: Éste es uno de los métodos más empleados en problemas difíciles como el nuestro.

• Análisis del peor caso: En este caso se consideran los ejemplos que sean más desfavorables para el algoritmo y se acota la máxima desviación respecto de la solución óptima. Esto acota el resultado para cualquier ejemplo, pero los resultados no suelen ser representativos para el comportamiento medio del algoritmo

Existen muchos métodos heurísticos, lo que es complicado dar una clasificación de ellos. Además muchos han sido diseñados para un problema específico, luego nos centraremos en algunos que nos interesan para nuestro problema y más conocidos ya que abordarlos todos sería demasiado largo.

Métodos constructivos

Consisten en construir paso a paso una solución del problema. Son métodos deterministas y suelen estar basados en la mejor elección en cada iteración. Ahora hablaremos de los metodos constructivos más conocidos:

Heurístico del vecino más próximo

Trata de construir un ciclo Hamiltoniano de bajo coste basándose en el vértice cercano a uno dado. Este algoritmo es debido a Rosenkrantz, Stearns y Lewis. Esta heurística se basa en la idea de moverse de una ciudad a la siguiente, de tal forma que, de todas las opciones, la ciudad elegida sea la más cercana a donde se encuentra el viajero, es decir seleccionando aristas de bajo coste.

Es una heurística miope, es decir, en una iteración escoge la mejor opción que tiene disponible, sin ver que esto puede obligarle a tomar malas decisiones posteriormente; al final del proceso probablemente quedarán vértices cuya conexión obligará a introducir aristas de coste elevado.

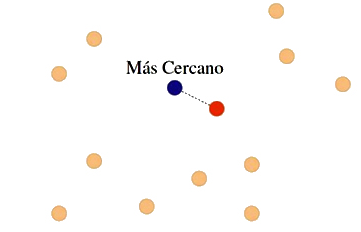
Algoritmo

• Inicialización
  • Seleccionar un vértice \( j \) al azar
  • Hacer \( t=j \) y \( W=V \setminus \{j\} \)
• Mientras \( (W \neq \phi ) \)
  • Tomar \( j \) de \( W | c_{tj} = min \{c_{ti} / i \in W \} \)
  • Conectar \( t \) a \( j \)
  • Hacer \( W = W \setminus \{j\} \) y \( t =j \)

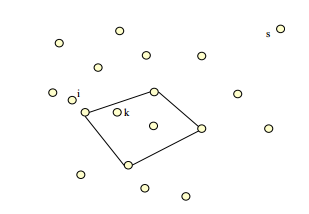
Heurísticos de inserción

Consiste en comenzar construyendo ciclos que visiten únicamente unos cuantos vértices, para posteriormente extenderlos insertando los vértices restantes. En cada paso se inserta un nuevo vértice en el ciclo hasta obtener un ciclo Hamiltoniano. Este algoritmo también es debido a Rosenkrantz, Stearns y Lewis.

Algoritmo

• Inicialización
  • Seleccionar un ciclo inicial (subtour) con \( k \) vértices
  • Hacer \( W = V \setminus \{ \) vertices seleccionados \( \} \)
• Mientras \( (W \neq \phi ) \)
  • Tomar \( j \) de \( W \) de acuerdo con algún criterio preestablecido
  • Insertar \( j \) donde menos incremente la longitud del ciclo
  • Hacer \( W = W \setminus \{ j \} \)

Los criterios más utilizados son:

• Inserción más cercana: Seleccionar el vértice \( j \) más cercano al ciclo \( d_{\min} (j) = \min \{ d_{min} (v) / v \in W \}\)
• Inserción más lejana: Seleccionar el vértice \( j \) más lejano al ciclo \( d_{\min} (j) = \max \{ d_{\min} (v) / v \in W \} \)
• Inserción más barata: Seleccionar el vértice \( j \) con el menor incremento del coste
• Inserción aleatoria: Seleccionar el vértice \( j \) al azar
  

Métodos de búsqueda local

El procedimiento de búsqueda o mejora local, comienza con una solución del problema y permite ir mejorando la solución actual mientras se pueda. El algoritmo se detiene cuando la solución no puede ser mejorada. A la solución encontrada se le denomina óptimo local. Este criterio es conocido como greedy.

El óptimo local alcanzado no puede mejorarse mediante el movimiento definido, pero esto no permite garantizar que sea el óptimo global del problema. Dada la miopía de la búsqueda local, es de esperar que en algunos problemas no lo sea. Ahora hablaremos de los métodos de búsqueda local más conocidos:

Procedimientos de 2 intercambios

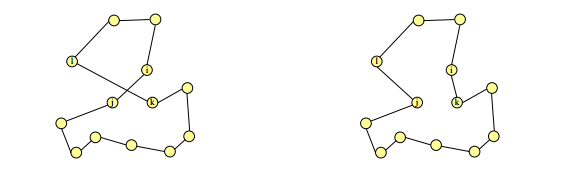
Algoritmo

• Inicialización
  • Considerar un ciclo Hamiltoniano inicial
  • \( movimiento = 1 \)
    
• Mientras (\( movimiento = 1 \))
  • \( movimiento=0 \). Etiquetar todos los vértices como no explorados
  • Mientras (queden vértices por explorar)
    • Seleccionar un vértice \( i \) no explorado
    • Examinar todos los movimientos 2-opt que incluyan la arista de \( i \) a su sucesor en el ciclo
    • Si alguno de los movimientos examinados reduce la longitud del ciclo, realizar el mejor de todos y hacer \( movimiento = 1 \).
    • En otro caso etiquetar \( i \) como explorado
La variable \( movimiento \) vale 0 si no se ha realizado ningún movimiento al examinar todos los vértices, y 1 en otro caso. El algoritmo finaliza cuando \( movimiento = 0 \), con lo que queda garantizado que no existe ningún movimiento 2-opt que pueda mejorar la solución.




Procedimientos de k-intercambios


Para introducir mayor flexibilidad al modificar un ciclo Hamiltoniano, podemos considerar el dividirlo en \( k \) partes, en lugar de dos, y combinar los caminos resultantes de la mejor manera posible. Llamamos movimiento k-opt a tal modificación.

Es evidente que al aumentar \( k \) aumentará el tamaño del entorno y el número de posibilidades a examinar en el movimiento, tanto por las posibles combinaciones para eliminar las aristas del ciclo, como por la reconstrucción posterior. El número de combinaciones para eliminar \( k \) aristas en un ciclo viene dado por el número \( n \choose k \). Esto hace que sólo pueda ser aplicado a ejemplos de tamaño pequeño.




Métodos combinados

Los métodos constructivos y los de búsqueda local pueden combinarse, tomando los segundos como solución inicial la obtenida con los primeros.