Formulación
En este apartado del trabajo vamos a ver algunas de las formulaciones más utilizadas para resolver el problema del viajante de comercio. Previamente definiremos las dos versiones que existen del problema. Podemos tener en cuenta dos:
Simétrico: donde la distancia entre un par de ciudades es la misma tome el sentido que se tome. En este caso la matriz de coste sería simétrica.
Asimétrico: donde la distancia puede ser diferente a la ida que a la vuelta e incluso no existir una de ellas. En este caso la matriz de costes no es simétrica.
Para enunciar el problema formalmente introducimos la siguiente terminología: sea un grafo \( G=(V,A,C) \) donde \( V \) es el conjunto de vértices, \( A \) es el de aristas y \( C=(c_{ij}) \) es la matriz de costes, es decir, \( c_{ij} \) es el coste o distancia de la arista \( (i, j) \).
Un camino es una sucesión de aristas \( (e_1, e_2, \ldots, e_k) \) en donde el vértice final de cada arista coincide con el inicial de la siguiente.
Un camino es simple si no utiliza el mismo vértice mas de una vez
Un ciclo es un camino \( (e_1, e_2, \ldots, e_k) \) en el que el vértice final de \( e_k \) coincide con el inicial de \( e_1 \)
Un ciclo es simple si lo es el camino que lo define
Un subtour es un ciclo simple que no pasa por todos los vértices del grafo
Un tour o ciclo hamiltoniano es un ciclo simple que pasa por todos los vértices del grafo
El Problema del Viajante consiste en determinar un tour de coste mínimo.
Para que nos quede claro, la figura siguiente muestra un grafo de 8 vértices en el que aparece destacado un ciclo hamiltoniano.
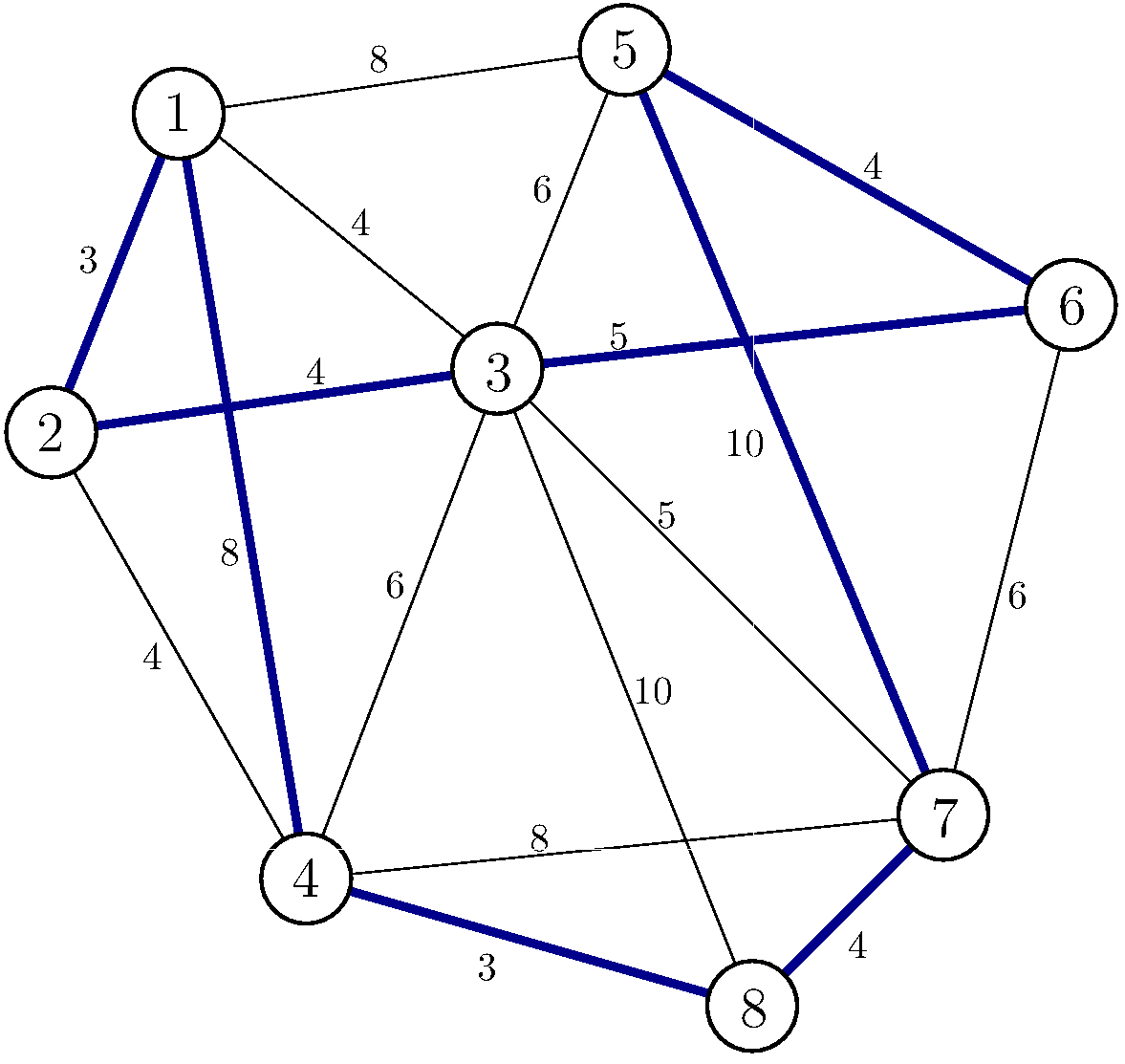
Debemos considerar que el grafo es completo, es decir, que para cada par de vértices existe una arista que los une. De no ser así, siempre podemos añadir una arista ficticia entre dos vértices con el coste del camino más corto que los une. Así por ejemplo, en el grafo de la figura podemos añadir una arista entre los vértices 1 y 6 con coste 9 correspondiente al camino 1-3-6. Este problema puede ser escrito como un grafo donde los vértices se corresponden con las ciudades, los caminos entre ciudades con las aristas y los valores de las distancias con los pesos de las aristas. Por tanto enumeramos las ciudades de 1 a \( n \), consideramos que \( x_{ij} \) represente la arista que va del vértice \( i \) al \( j \), tomando el valor 1 si la arista del vértice \( i \) al \( j \) está en la solución y 0 en caso contrario. Por último, el coste de la distancia lo designamos como \( c_{ij} \). Si no existe arista del vértice \( i \) al \( j \), para los cálculos le asignamos un número arbitrariamente grande e igualmente para los costos \( c_{ii} \) de tal forma que no exista en la solución la posibilidad de que \( x_{ii}=1 \), es decir, para imponer que \( x_{ii}=0 \).
Como estamos ante un problema donde queremos que las sumas de las distancias sea la menor posible tenemos que la función objetivo es: $$\min\sum_{i=1}^{n} \sum_ {j=1}^{n} c_{ij} x_{ij}$$
Sujeto a las siguientes restricciones: $$\sum_{j=1}^{n}x_{ij}=1$$ $$\sum_{i=1}^{n}x_{ij}=1$$
La 1ª restricción implica que de cada ciudad se salga una vez y la 2ª restricción implica que a cada ciudad se llegue una sola vez.
Estas restricciones no son suficientes ya que se pueden dar caminos disjuntos o lazos parciales tales que no se satisficiesen las condiciones del problema. Por ejemplo con 5 ciudades podríamos obtener como solución \( x_{15}=x_{23}=x_{32}=x_{54}=x_{41}=1 \) y el resto de \( x_{ij} \) con valor 0 que como vemos en la imagen corresponde con dos caminos disjuntos.
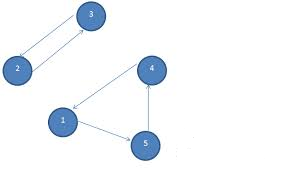
Una posible solución para romper estos lazos es añadir las siguientes restricciones:
- Para evitar los lazos de orden 2: \( x_{ij}+x_{ji}\leq 1 \) para todo \( i, j \)
- Para evitar los lazos de orden 3: \( x_{it}+x_{tj}+x_{ji}\leq 2 \) para todo \( i, j, t \)
- Para evitar los lazos de orden 4: \( x_{it}+x_{tp}+x_{pj}+x_{ji} \leq 3 \) para todo \( i, j, p, t \). Así sucesivamente hasta evitar los lazos de orden \( n/2 \) ya que no existen lazos de orden mayor, por ejemplo, en 8 ciudades no existen lazos de orden 6 pues implicaría que hubiera uno de orden 2 y esto no es posible.
Otra forma de romper estos lazos es a través de variables de decisión \( u_{i} \) que representa la posición en la que se visita la ciudad \( i \) (pues con los lazos no se podría establecer que vértices se visitaron antes o después), estos tomarían los valores del 1 al \( n \) siendo \( u_{1}=1 \) pues sería la primera ciudad en visitar, con la restricción: \( u_{i}-u_{j}\leq (n-1)(1-x_{ij})-1 \) para todo \( i \), \( j \). Si vamos de la ciudad \( i \) a la \( j \) directamente tenemos que \( x_{ij}=1 \) y \( u_{i}-u_{j} = -1 \leq 0 \) y si vamos de la ciudad \( i \) a la \( j \) pasando por otras ciudades tenemos que \( x_{ij}=0 \) entonces \( u_{i}-u_{j}\leq (n-1) \), por tanto se cumple la inecuación ya que la diferencia máxima entre \( u_{i} \) y \( u_{j} \) es \( n-1 \), que es el caso en que \( u_{1}=1 \) y \( u_{k}=n \). Con el primer caso de ruptura de lazos se requieren \( 2^{n}+2n-2 \) restricciones en total y en el segundo caso se requieren \( n^2-n+2 \) restricciones, por lo que en el segundo caso tenemos menos restricciones pero tenemos más variables.